Exterior angle theorem

Exterior angle theorem

The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. 

Video: External Angle Theorem

In several high school treatments of geometry, the term "exterior angle theorom" has been applied to a different result, namely the portion of Proposition 1.32 which states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. This result, which depends upon Euclid's parallel postulate will be referred to as the "High school exterior angle theorem" (HSEAT) to distinguish it from Euclid's exterior angle theorem.

Exterior angles

Video: Exterior Angles of a Polygon

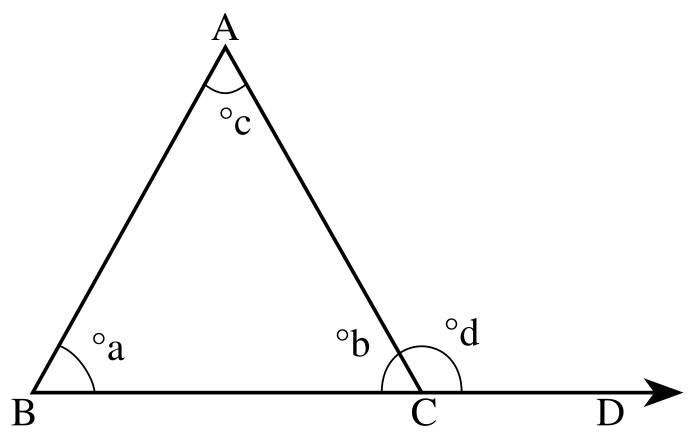
A triangle has three corners, called vertices. The sides of a triangle (line segments) that come together at a vertex form two angles (four angles if you consider the sides of the triangle to be lines instead of line segments). Only one of these angles contains the third side of the triangle in its interior, and this angle is called an interior angle of the triangle. In the picture below, the angles ∠ABC, ∠BCA and ∠CAB are the three interior angles of the triangle. An exterior angle is formed by extending one of the sides of the triangle; the angle between the extended side and the other side is the exterior angle. In the picture, angle ∠ACD is an exterior angle.

Euclid's exterior angle theorem

The proof of Proposition 1.16 given by Euclid is often cited as one place where Euclid gives a flawed proof.

Euclid proves the exterior angle theorem by:

• construct the midpoint E of segment AC,
• draw the ray BE,
• construct the point F on ray BE so that E is (also) the midpoint of B and F,
• draw the segment FC.

By congruent triangles we can conclude that ∠ BAC = ∠ ECF and ∠ ECF is smaller than ∠ ECD, ∠ ECD = ∠ ACD therefore ∠ BAC is smaller than ∠ ACD and the same can be done for the angle ∠ CBA by bisecting BC.

The flaw lies in the assumption that a point (F, above) lies "inside" angle (∠ ACD). No reason is given for this assertion, but the accompanying diagram makes it look like a true statement. When a complete set of axioms for Euclidean geometry is used (see Foundations of geometry) this assertion of Euclid can be proved.

High school exterior angle theorem

Video: Exterior Angle Theorem (High School EAT) | Two Opposite Interior Angles Add to the Exterior Angle

The high school exterior angle theorem (HSEAT) says that .....

‹ Angle           up           Exterior angle theorem video ›